Altitude of Triangle

A triangle and a parallelogram are constructed on the same base such that their areas are equal. If the altitude of the parallelogram is $100 \mathrm{m}$, then the altitude of the triangle is?

In $∆\mathrm{ABC}$, $\angle A<\angle B$, the altitude to the base divides vertex angle $C$ into two parts $C_1$ and $C_2$ adjacent to $BC$, then which one of the relation can be obtained?

In triangle $\mathrm{PQR},\mathrm{PS}$ is the altitude to $\mathrm{QR}$. Which of the following must be true?

The point $"H"$ in the given triangle $ABC$ is

Orthocentre is a

The point of intersection of the altitudes of a triangle is

The number of altitudes of a triangle is

Explain about the altitude of a triangle.

The orthocenter of a right-angled triangle is formed

The orthocentre of an acute angled triangle is

The orthocentre of an obtuse angled triangle is

The orthocentre of a triangle is determined by

Derive the formula for altitude of an isosceles triangle.

Define altitude of a triangle. Write its properties.

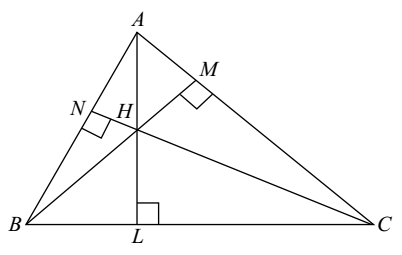
In the above figure, $AD, BE$ and $CF$ are the altitudes of the $△ABC$ and they meet at the point $O$. Therefore, $O$ is 

Incentre of a triangle is defined as the point where the three altitudes of a triangle meet.

_____ of a triangle is defined as the point where the three altitudes of a triangle meet.

Define orthocentre of a triangle.

The _____ triangle has its all the medians and altitudes of same length.

Number of points where the three heights (altitudes) of a triangle meet each other.